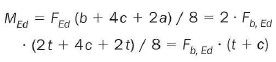Contenidos
 | Nota: Este artículo ha sido creado gracias a la Associació de Consultors d’Estructures en el marco del Programa de Afiliados de la Construpedia. El contenido está disponible en el sitio web de ACE ¡Atención! Esté artículo está sujeto a Derecho de Autor. |
|---|
Antecedentes
Hasta la aparición del Códiigo Técnico, la normativa española de estructuras de acero (la última, la NBE-EA-95) no hacía referencia explícita al diseño y el cálculo de los pasadores de las uniones articuladas. En el caso de las estructuras ligeras éste es un tipo de detalle muy utilizado.
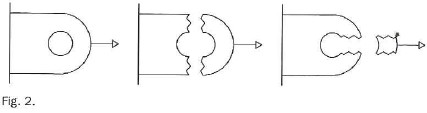
Incluso, tal y como se puede apreciar en las imágenes precedentes de la figura 1, podemos diferenciar claramente entre los pasadores de uniones comprimidas (la base del pilar) y de uniones traccionadas (el anclaje a la pared).
La forma tradicional de calcular estos detalles era la de considerar esta unión como ejemplo paradigmático de esfuerzo cortante, Normalmente, se intenta que la placa central esté lo más ajustada posible a las placas laterales, evitando así los esfuerzos de flexión, de forma que sólo haga falta comprobar el cortante sobre el pasador y el aplastamiento de las placas en contacto con el pasador. Sería el caso de la base del pilar.
Otras veces, por razones constructivas, la placa central quedaba lo suficiente separada de las placas laterales, de forma que la flexión del pasador no es despreciable. En estos casos hay que añadir a los análisis anteriores el esfuerzo de flexión sobre el pasador. Sí además el detalle de la articulación está traccionado, habrá que comprobar que las placas no se rompen alrededor del agujero. Sería el caso del detalle de la derecha, corres pon- diente a un anclaje a la pared (fig. 2).
El Eurocódigo 3: Proyecto de estructuras de acero (1993) introduce un apartado exclusivo para el diseño y cálculo de estas placas y pasadores, es el 6.5.13, Uniones con pasadores. Como no está la obligatoriedad de esta norma, pienso que ha pasado algo desapercibida la puesta en práctica de estas recomendaciones que, como veremos, pueden dar lugar, cuando menos, a situaciones algo incongruentes.
El Código Técnico, en su libro 4, DB SE-A Seguridad Estructural: Acero, en el apartado 8.5.4 Pasadores, resume minuciosamente el texto del Euro- código, con unas pequeñas variaciones de la formulación que no representan ningún cambio en absoluto.
CTE, SE-A , 8.5.4 Pasadores
La comprobación del diseño de una unión articulada con pasador viene determinada por el cumplimiento de cuatro verificaciones:
1. La resistencia a cortante del pasador.
2. La resistencia a flexión del pasador.
3. La resistencia al esfuerzo combinado de cortante y flexión sobre el pasador.
4. La resistencia al aplastamiento de la placa.
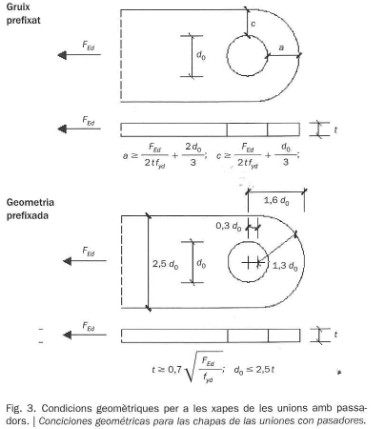
No dice nada de la resistencia a tracción o a cortante de las placas alrededor del agujero, pero sí que fija unas condiciones geométricas, de las cuales sólo hace falta cumplir una, para las placas de las uniones con pasadores que, de hecho, son el resultado de aplicar este esfuerzos de tracción y cortante alrededor del agujero.
Es interesante observar una cierta incongruencia en la segunda condición, la denominada «Geometría prefijada», puesto que partiendo de una geometría basada con el diámetro del agujero d0 acaba definiendo el propio diámetro del agujero en la d0 <= 2,5 t. No sabemos muy bien si propone un proceso iterativo donde hace falta ir tanteando un valor d0 hasta que cumpla con esta condición t >= d0/2,5.
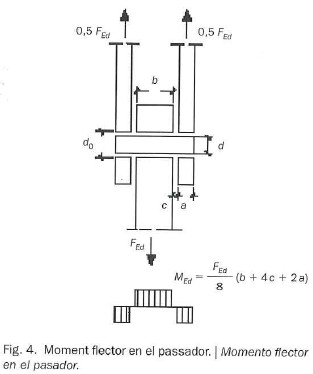
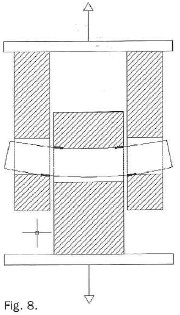
Dice también que los esfuerzos en el pasador y en cada una de las placas se calculará a partir de las distribuciones de tensiones indicadas en la figura 4.
En un primer vistazo, esta distribución de tensiones puede parecer lógica puesto que el pasador suele ser una pieza muy rígida que no se deforma y, por lo tanto, la distribución de tensiones en la zona de contacto se puede considerar uniforme.
Sin embargo, veremos más adelante que en determinadas ocasiones esta consideración no es del todo acertada, puesto que da lugar a resultados algo extraños, sobre todo cuando los grosores de las placas son más grandes que lo estrictamente necesarios.
Si do nos encontramos delante de una caso de cortante puro. La normativa sigue obligando a calcular el pasador a esfuerzos de flexión, lo que ya se ve que se trata de un absurdo.
Es también interesante fijarse en el hecho que para el cálculo de la resistencia a cortante del pasador se utiliza la resistencia última del acero del pasador fub:
mientras que para el cálculo de la resistencia a flexión del pasador se utiliza la tensión del límite elástico del acero del pasador fyb:
siempre con un coeficiente de seguridad YM2 = 1,25.
Una aplicación concreta
Para concretar en la exposición que estamos llevando a cabo, resolveremos un ejemplo que nos ayude a interpretar
estas reflexiones sobre la bondad de la normativa aplicable.
Suponemos un detalle de articulación que debe soportar una acción mayorada de FED = 60 kN. Utilizamos un acero para el pasador S355 y un acero para las placas 5275.
En primer lugar calculamos el diámetro del pasador para que soporte el esfuerzo a cortante. Con un diámetro de 19 mm el pasador soporta una acción de:
Con este diámetro podemos definir el grosor de la placa central para que no se produzca el aplastamiento de la placa. Una placa de 10 mm es suficiente, puesto que soporta una acción de:
Por lo tanto, las placas laterales sólo haría falta que fueran de 5 mm de grosor, puesto que la reacción en cada una de ellas es la mitad que la acción.
Intentamos poner las placas laterales lo más cerca posible de la placa central, es decir 1 mm de margen (que realmente es muy ajustado, incluso quizás demasiado).
a grosor de la placa lateral = 5 mm
b grosor de la placa central 10 mm
c separación entre placas 1 mm
Bien. Con estas medidas de placas ya podemos calcular el momento (lector que actúa sobre el pasador que es igual, según la normativa, a:
Mientras que el momento que aguanta el pasador sólo es de:
Dado que el pasador no es capaz de soportar el momento MEd hará falta aumentar el diámetro del pasador.
Con un pasador de diámetro 21 mm, el momento que soporta es de 200,8 kNmm, por lo tanto ya es suficiente. Aun así, al combinar los esfuerzos de cortante y flexión obtenemos un valor de 1,39 que supera la unidad, que es el valor máximo admisible. Debemos seguir aumentando, pues, el diámetro del pasador.
Con un pasador de 23 mm tenemos:
0,64 Resistencia a cortante del pasador:
93,73 kN.
0,68 Resistencia a flexión del pasador:
263,7 kNmm.
0,88 Resistencia al esfuerzo combinado
de cortante y flexión sobre el pasador.
0,79 Resistencia al aplastamiento de la placa:
75,9 kN.
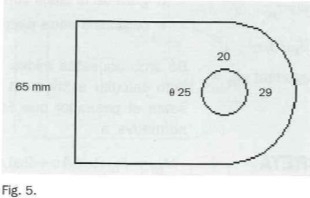
Dado que ya hemos fijado el grosor de las placas, podemos dibujar la geometría mínima en función del agujero de la placa para el pasador, que podemos suponer de 25 mm (23 + 2) mm.
Hasta aquí el proceso seguido por la normativa es impecable. Sin embargo, ya hemos visto cómo ha sido la flexión el esfuerzo determinante del cálculo, aun cuando hemos ajustado mucho las placas entre ellas y parecía que habría de haber sido el esfuerzo cortante el que debía ser determinante.
Incluso, si suponemos las placas con una distancia cero entre ellas, es decir, frotándose unas con las otras, y el pasador colocado en un agujero del mismo diámetro, lo cual es la forma normal de hacer un ensayo a esfuerzo cortante puro, el pasador baja a un diámetro de 22 mm, pero vemos que todavía la flexión representa casi la mitad de la capacidad resistente de la unión:
0,70 Cortante en el pasador.
0,65 Flexión en el pasador.
0,91 Esfuerzo combinado de flexión
y cortante.
0,83 Aplastamiento de la placa.
Seguimos con el ejercicio de interpretación del resultado y volvemos al caso original con los datos siguientes:
23 mm Diámetro del pasador.
10 mm Placa central.
5 mm Placas laterales.
1 mm Separación entre placas.
Aumentaremos la separación entre placas puesto que consideramos, por ejemplo, que un margen de 1 mm a cada lado (2 mm en total) es demasiado justo. Aplicaremos un margen de 2,5 mm a cada lado (5 mm en total).
Vemos que no cumple la normativa debido al esfuerzo combinado de flexión y cortante:
0,64 Cortante en el pasador.
0,86 Flexión en el pasador.
1,14 Esfuerzo combinado de flexión y cortante.
0,79 Aplastamiento de la placa.
Hace falta aumentar el pasador a 24 mm y obtene
mos:
0,59 Cortante en el pasador.
0,75 Flexión en el pasador.
0,91 Esfuerzo combinado de flexión y cortante.
0,76 Aplastamiento de la placa.
Parece lógico que, al aumentar la separación entre placas, aumente la flexión del pasador y nos obligue a aumentar el diámetro. ¿Qué pasaría si aumentáramos, por la razón que sea, el grosor de la placa central? Probamos de colocar una placa central de 15 mm y vemos cómo, debido al aumento de la flexión, la combinación de esfuerzos vale 11,1>1,00 y hace falta aumentar el diámetro del pasador.
0,54 Cortante en el pasador.
0,78 Flexión en el pasador.
0,89 Esfuerzo combinado de flexión y cortante.
0,48 Aplastamiento de la placa.
Observamos cómo los valores de resistencia a cortante y el aplastamiento pasan a ser unos valores secundarios puesto que a duras penas superan un valor de 0,5. Bien, todavía podríamos entender este aumento pensando que al hacer más gruesa la placa central ha aumentado la longitud útil del pasador y por lo tanto su flexión. El paso siguiente será aumentar el grosor de las placas laterales a un valor de 10 mm. La resistencia a flexión aumenta a 1,00 (todavía válida) pero la combinación de esfuerzos alcanza el valor de 1,29. Hace falta aumentar el grosor del pasador a 27 mm.
0,46 Cortante en el pasador.
0,79 Flexión en el pasador.
0,84 Esfuerzo combinado de flexión y cortante.
0,45 Aplastamiento de la placa.
En este caso la reflexión es más compleja puesto que cuesta mucho creer que aumentando el grosor de las placas exteriores el sistema aguante menos que con unas placas más delgadas. ¿Qué pasaría si las placas exteriores fueran una pieza perteneciente a una máquina y tuvieran un grosor gordo, como por ejemplo 50 mm? Pues sencillamente habríamos de aumentar el grosor del pasador hasta 36 mm.
0,26 Cortante en el pasador.
0,93 Flexión en el pasador.
0,93 Esfuerzo combinado de flexión y cortante.
0,36 Aplastamiento de la placa central.
En este caso hemos llegado al absurdo de que el esfuerzo cortante pasa a ser meramente testimonial con un valor de repercusión de sólo 0,26 y el valor del esfuerzo combinado es igual que el de flexión.
Explicación
La razón de este absurdo reside en el hecho de que la normativa calcula el momento flector que afecta el pasador a partir de la suposicíón que las reacciones del pasador sobre las placas laterales y central son uniformes, tal y como se muestra en la figura 4 deI Código Técnico (más arriba en este mismo texto). Con esta premisa cualquier aumento del grosor de cualquier placa tiene el mismo efecto que el aumento de la separación entre placas.
Según nuestro criterio, esto es un error. A continuación analizaremos el porqué.
Si el pasador se ve sometido a un esfuerzo de flexíón que puede llegar a ser mucho más importante que el esfuerzo obvio de cortante, tendremos que considerar también la deformación del pasador bajo esfuerzo de flexión. Incluso podríamos estudiar la deformación del pasador bajo esfuerzo cortante, puesto que se trata de una barra corta y en este caso esta deformación puede no ser despreciable, pero por el momento no creemos que sea necesario.
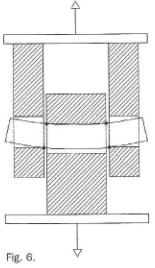
Cuando el pasador se defornia por flexión, deja de tener contacto uniforme con el grosor de las placas y las reacciones dejan de ser uniformes por concentrarse en cuatro puntos: las caras ínteriores de las placas laterales y las caras exteriores de la placa central (flg. 6).
Con esta nueva configuración de reacciones el momento máximo aplicado en el pasador deja de ser:
tal y como define el Código Técnico y pasa a tener un valor máxímo de:
es decir un valor que sólo depende de la separación entre placas, lo cual se acerca más al que el sentido constructivo del sistema nos hacía pensar y que ya hemos comentado con anterioridad. Con este criterio, una vez definidos los grosores mínimos de las placas laterales y central, podemos aumentar los mencionados grosores sin que esto implique ningún aumento del momento y por lo tanto ningún aumento del diámetro del pasador.
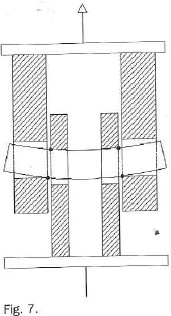
De hecho esta interpretación no deja de ser una constatación del diseño antiguo que aconseja hacer sistemas articulados con dos placas centrales separadas y dos placas laterales, en aquellos casos en que, por alguna razón, las placas laterales han de estar muy separadas. Este sistema de doble placa central se ha utilizado mucho también en las estructuras tensadas que hemos mencionado a principios de este texto (Fig. 7).
Una mayor precisión en el diseño
Ya se ve que la consideración que se ha hecho en el apartado anterior peca algo de simplista, puesto que la reacción nunca puede estar situada en un punto. Un punto no tiene dimensiones y, por lo tanto, la tensión sobre el acero de la placa sería infinita.
En este caso la placa se aplastaría y la zona de contacto aumentaría. Por lo tanto, las reacciones producidas dejarían de ser cuatro fuerzas aplicadas en cuatro puntos para reproducir unas tensiones uniformes en la zona de aplastamiento debido a la presión existente.
Curiosamente, si hemos diseñado un grosor mínimo de las placas para evitar el aplastamiento, tendremos que el momento flector es el que fija el Código Técnico, puesto que el grosor de las placas coincide en la zona de aplastamiento:
pero este momento se mantiene aunque aumentemos el grosor de las placas, tanto las laterales como la central, puesto que las zonas de contacto por aplastamiento del punto teórico mencionado en el apartado anterior será siempre el mismo: «a» la placa lateral y «b/2» a la placa central. Estas zonas de contacto se situarán también en las caras interiores de las placas laterales y en las caras exteriores de la placa central. Si el tipo de acero es igual en las placas laterales y en la placa central, entonces a = b/2.
Incluso en el supuesto de que hubiera dos placas centrales, independientemente de su grosor, la zona de contacto será siempre la misma.
Así pues, proponemos la modificación siguiente del Código Técnico y del Eurocódigo.
El grosor mínimo t de la placa lateral para evitar el aplastamiento (suponiendo siempre que la calidad del acero del pasador es igual o mayor que la de las placas) es, según el propio Código Técnico.
A partir de aquí, el momento flector del pasador será:
Si, como parecería lógico, la placa lateral tiene un grosor igual a t y la placa central tiene un grosor igual a 2t, el valor del momento MEd coincide, tanto con la fórmula del Código Técnico como en la que se propone aquí.
Este momento será constante sea cual sea el grosor de las placas, tanto central como laterales, incluso si la placa central se desdobla en dos placas sitas junto a las laterales.
Comparativa de resultados
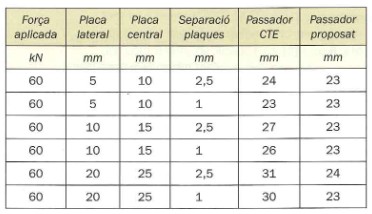
Aprovechando el mismo ejemplo que hemos utilizado en este texto tendremos:
dónde podemos apreciar que, para una misma fuerza aplicada de 60 kN, en función del grosor de las placas (siempre iguales o superiores a las necesarias) el diámetro del pasador puede oscilar fácilmente en 7 mm (30%) según se aplique la fórmula propuesta por la normativa [1] o la fórmula propuesta en este texto [2].
Hace falta hacer un comentario respecto a la tabla anterior, por el hecho de que, en el penúltimo caso, aparece un diámetro del pasador más grande. Resulta que cuando las placas superan los 16 mm, el límite elástico del material de las placas baja y por esto aumenta el grosor mínimo de la placa (zona de aplastamiento), con lo cual aumenta el momento flector del pasador y, consecuentemente, el diámetro. En el último caso no es así por la precisión del cálculo.